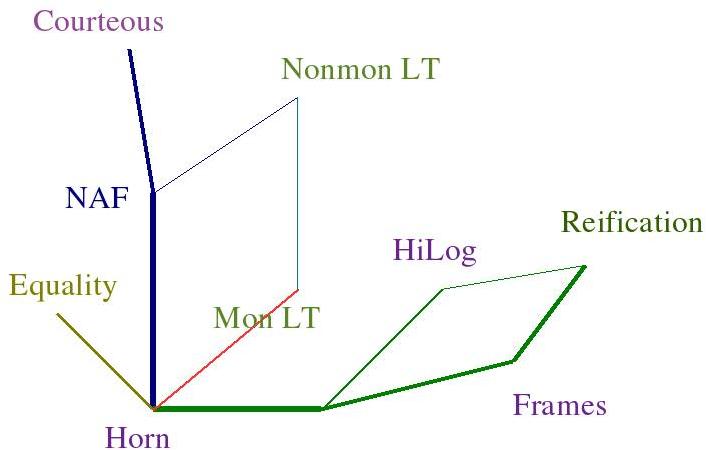
Figure 2.1: The Layered Structure of SWSL-Rules
As mentioned in the introduction, SWSL consists of two separate sublanguages, which have layered structure. This section gives an overview of these layers.
The SWSL-Rules language is designed to provide support for a variety of tasks that range from service profile specification to service discovery, contracting, policy specification, and so on. The language is layered to make it easier to learn and to simplify the use of its various parts for specialized tasks that do not require the full expressive power of SWSL-Rules. The layers of SWSL-Rules are shown in Figure 2.1.

Figure 2.1: The Layered Structure of SWSL-Rules
The core of the language consists of the pure Horn subset of SWSL-Rules. The monotonic Lloyd-Topor (Mon LT) extension [Lloyd87] of the core permits disjunctions in the rule body and conjunction and implication in the rule head. NAF is an extension that allows negation in the rule body, which is interpreted as negation-as-failure. More specifically, negation is interpreted using the so called well-founded semantics [VanGelder91]. The nonmonotonic Lloyd-Topor extension (Nonmon LT) further permits quantifiers and implication in the rule body. The Courteous rules [Grosof99a] extension introduces two new features: restricted classical negation and prioritized rules. HiLog and Frames extend the language with a different kind of ideas. HiLog [Chen93] enables high degree of meta-programming by allowing variables to range over predicate symbols, function symbols, and even formulas. Despite these second-order features, the semantics of HiLog remains first-order and tractable. It has been argued [Chen93] that this semantics is more appropriate for many common tasks in knowledge representation than the classical second-order semantics. The Frames layer of SWSL-Rules introduces the most common object-oriented features, such as the frame syntax, types, and inheritance. The syntax and semantics of this extension is inspired by F-logic [Kifer95] and the followup works [Frohn94, Yang02, Yang03]. Finally, the Reification layer provides a mechanism for making objects out of a large class of SWSL-Rules formulas, which puts such formulas into the domain of discourse and allows reasoning about them.
All of the above layers have been implemented in one system or another and have been found highly valuable in knowledge representation. For instance, FLORA-2 [Yang04] includes all layers except Courteous rules and Nonmonotonic Lloyd-Topor. SweetRules [Grosof2004b] supports Courteous extensions, and Ontobroker [Ontobroker] supports Nonmonotonic Lloyd-Topor and frames.
Four points should be noted about the layering structure of SWSL-Rules.
naf, for
negation-as-failure, and neg, for classical negation.
Likewise, it distinguishes between the classical
implication, <== and
==>, and the if-then connective :- used
for rules.
SWSL-FOL is used to specify the dynamic properties of services, namely, the processes that they are intended to carry out. SWSL-FOL also has layered structure, which is depicted in Figure 2.2.
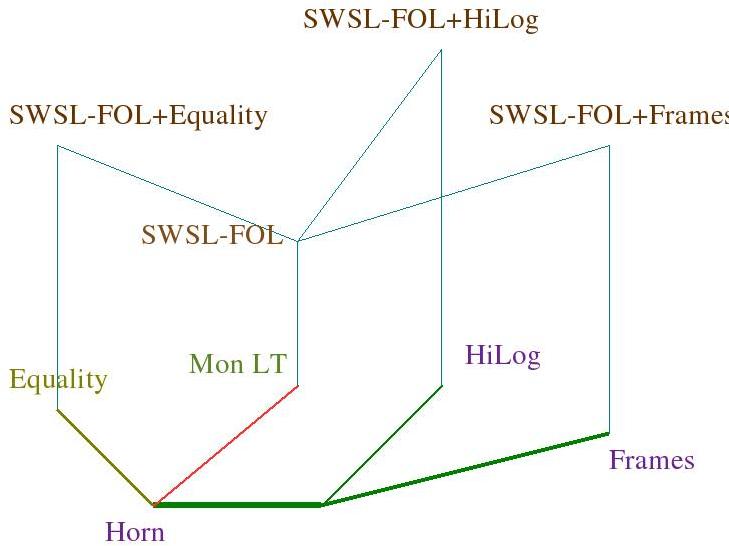
Figure 2.2: The Layers of SWSL-FOL and Their Relationship to SWSL-Rules
The bottom of Figure 2.2 shows those layers of SWSL-Rules that have monotonic semantics and therefore can be extended to full first-order logic. Above each layer of SWSL-Rules, the figure shows corresponding SWSL-FOL extension. The most basic extension is SWSL-FOL. The other three layers, SWSL-FOL+Equality, SWSL-FOL+HiLog, and SWSL-FOL+Frames extend SWSL-FOL both syntactically and semantically. Some of these extensions can be further combined into more powerful FOL languages. We discuss these issues in Section SWSL-FOL: The First-order Subset of SWSL.
In this section we define the basic syntactic components that are common to all layers of SWSL-Rules. Additional syntax will be added as more layers are introduced.
A constant is either a numeric value, a symbol, a string, or a URI.
123,
34.9, 45e-11. See
the section on SWSL data types for more details
on the relationship between SWSL data types and
the
primitive data types in XML Schema.
'abc#$%'. Single quotes that are
part of a symbol are escaped with the backslash. For instance, the
symbol a'bc''d
is represented as 'a\'bc\'\'d'. The backslash is escaped with
another backslash. Symbols that consist
exclusively of alphanumeric characters and the underscore (_)
and begin with a letter or an underscore do not need to be quoted.
"ab'%#cd". A double quote
symbol that
occurs in a string must be escaped with the backslash. For instance, the
string ab"cd"""gf
is represented as "ab\"cd\"\"\"gf".
A full URI is a sequence of characters that has the form of
a URI, as specified by IETF, and is enclosed between _"
and ".
For instance, _"http://w3.org/".
An sQName has the form prefix#local-name. Here prefix is an alphanumeric symbol that is defined to be a shortcut for a URI as specified below; local-name is a string that must be acceptable as a path component in a URI. If local-name contains non-alphanumeric symbols, it must be enclosed in double quotes: e.g., "ab%20". An sQName is treated as a macro that expands into a full URI by concatenating the expansion of prefix (the URI represented by the prefix) with local-name. For the rationale behind the use of sQName see the entry for sQName in the Glossary.
A prefix declaration is a statement of the form
prefix prefix-name = "URI".
The prefix can then be used instead of the URI in sQNames. For instance, if we define
prefix w3 = "http://www.w3.org/TR/".
then the SWSL-URI _"http://www.w3.org/TR/xquery/" is considered
to be equivalent to w3#"TR/xquery/"
A variable is an alphanumeric symbol (plus the underscore), which
is prefixed with the ?-sign. Examples: ?_,
?abc23.
A first-order term is either a constant, a variable, or an
expression of the form t(t1,...,tn),
where t is a constant
and t1,...,tn are
first-order terms. Here the constant t is said to be used as a
function symbol and t1,...,tn are
used as arguments.
Variable-free terms are also called ground.
Following Prolog, we also introduce special notation for lists:
[t1,...,tn] and
[t1,...,tn|rest], where
t1,...,tn and rest are
first-order terms. The first form shows all the elements of the list
explicitly and the latter shows explicitly only a prefix of the list and uses
the first-order term rest to represent the tail.
We should note that, like in Prolog, this is just a convenient shorthand
notation. Lists are nothing but first-order terms that are representable with
function symbols. For instance, if cons denotes a function symbol
that prepends a term to the head of a list then [a,b,c] is
represented as first-order term cons(a,cons(b,c)).
A first-order atomic formula has the same form as first-order terms except that a variable cannot be a first-order atomic formula. We do not distinguish predicates as a separate class of constants, as this is usually not necessary, since first-order atomic formulas can be distinguished from first-order terms by the context in which they appear.
As many other rule-based languages, SWSL-Rules has a
special unification operator, denoted =.
The semantics of the unification operator is fixed and therefore
it cannot appear in a rule head.
An atomic formula of the form
= term2
where both terms are ground, is true if and only if the two terms are
identical. If term1 and term2
have variables, then an occurrence of the above formula in a rule body is
interpreted as a test of whether a substitution exists that can make the
two terms identical. The = predicate is related to the
equality predicate :=: introduced by
the Equality Layer, which is discussed
later.
To test that two terms do not unify SWSL-Rules uses the
disunification operator !=. For ground
terms, term1 != term2
iff the two terms are not identical. For non-ground terms, this is
true if the two terms do not unify.
A conjunctive formula is either an atomic formula or a formula of the form
and conjunctive formula
where and is a conjunction connective.
Here and henceforth in similar definitions, italicized words will be
meta-symbols that denote classes of syntactic entities.
For instance, atomic formula above means ``any
atomic formula.''
An and/or formula is either a conjunctive formula or a
formula of either of the forms
or and/or formula
and and/or formula
In other words, an and/or formula can be an arbitrary Boolean combination of
atomic formulas that involves the connectives and
and or.
Comments. SWSL-Rules has two kinds of comments: single line
comments and multiline comments. The syntax is the same as in Java.
A single-line comment is any text that starts with
a // and continues to the end of the current
line. If // starts within a string ("...") or a symbol ('...')
then these characters are considered to be part of the string or the symbol,
and in this case they do not start a comment. A multiline
comment begins with /* and end with a
matching */. The combination /* does not start a
comment if it appears inside a string or a symbol. The /*
- */ pairs can be nested and a nested occurrence
of */ does not close the comment. For instance, in
/* start /* foobar */ end */
only the second */ closes the comment.
A Horn rule has the form
head :- body.
where head is an atomic formula and body is a conjunctive formula.
A Horn query is of the form
?- query.
where query is a conjunctive formula.
Rules can be recursive, i.e., the predicate in the head of a rule can occur (with the same arity) in the body of the rule; or they can be mutually recursive, i.e., a head predicate can depend on itself through a sequence of rules.
All variables in a rule are
considered implicitly quantified with ∀
outside of the rule, i.e., ∀?X,?Y,...(head
:- body). A variable that occurs in the body of a rule but
not its head can be equivalently considered as being
implicitly existentially quantified in the body. For instance,
∀?X,?Y ( p(?X) :- q(?X,?Y) )
is equivalent to
∀?X ( p(?X) :- ∃?Y q(?X,?Y) )
Sets of Horn rules have the nice property that their semantics can be characterized in three different and independent ways: through the regular first-order entailment, as a minimal model (which in this case happens to be the intersection of all Herbrand models of the rule set) and as a least fixpoint of the immediate consequence operator corresponding to the rule set [Lloyd87].
This layer extends the Horn layer with three kinds of syntactic sugar:
A classical implication is a statement of either of the following forms:
formula1 ==> formula2
formula1 <== formula2
The Lloyd-Topor implication (abbr., LT implication) is a special case of the classical implication where the formula in the head is a conjunction of atomic formulas and the formula in the body can contain both conjunctions and disjunctions of atomic formulas.
A classical bi-implication is a statement of the form
formula1 <==> formula2
The Lloyd-Topor bi-implication (abbr., LT bi-implication) is a special case of the classical bi-implication where both formulas are conjunctions of atomic formulas.
The monotonic LT layer extends Horn rules in the following way. A rule still has the form
head :- body.
but head can now be a conjunction of atomic formulas and/or LT
implications (including bi-implications) and body can consist of
atomic formulas combined in arbitrary ways using the and and
the or connectives.
This extension is considered a syntactic sugar, since semantically any set of extended rules reduces to another set of pure Horn rules as follows:
head :- body1 or body2.
reduces to
head :- body1.
head :- body2.
head1 and head2 :- body.
reduces to
head1 :- body.
head2 :- body.
(head1 <== head2) :- body.
reduces to
head1 :- head2 and body.
(head1 ==> head2) :- body.
reduces to
head2 :- head1 and body.
Complex formulas in the head are broken down using the last three reductions. Rule bodies that contain both disjunctions and conjunctions are first converted into disjunctive normal form and then are broken down using the first reduction rule.
The NAF layer add the negation-as-failure symbol, naf.
For instance,
p(?X,?Y) :- q(?X,?Z) and naf r(?Z,?Y).
In SWSL-Rules we adopt the well-founded semantics [VanGelder91] as a way to interpret negation as failure. This semantics has good computational properties when no first-order terms of arity greater than 0 are involved, and the well-founded model is always defined and is unique. This model is three-valued, so some facts may have the ``unknown'' truth value.
We should note one important convention regarding the treatment of variables
that occur under the scope of naf and that do not occur anywhere
outside of naf in the same rule. The well-founded semantics was
defined only for ground atoms and the interpretation of unbound variables was
left open. Therefore, if Z does not occur elsewhere in the rule
then the meaning of
... :- ... and naf r(?X) and ...
can be defined as
... :- ... and ∃ X (naf r(?X)) and ...
or as
... :- ... and ∀ X (naf r(?X)) and ...
In practice, the second interpretation is preferred, and this is also a convention used in SWSL-Rules.
This layer introduces explicit bounded quantifiers (both exist
and forall), classical implication
symbols, <== and ==>, and the
bi-implication symbol <==> in the rule body. This essentially
permits arbitrary first-order-looking formulas in the body of SWSL-rules. We
say "first-order-looking" because it should be kept in mind that the
semantics of SWSL-Rules is not first-order and, for example,
classical implication A <== B is interpreted in a
non-classical way: as (A or naf B) rather than (A or neg
B) (where neg denotes classical negation).
Recall that without explicit quantification, all variables in a rule are
considered implicitly quantified with forall
outside of the rule, i.e., forall ?X,?Y,...(head
:- body). A variable that occurs in the body of a rule but
not its head can be equivalently considered as being
implicitly existentially quantified in the body. For instance,
forall ?X,?Y ( p(?X) :- q(?X,?Y) )
is equivalent to
forall ?X ( p(?X) :- exist ?Y q(?X,?Y) )
In the scope of the naf operator, unbound variables have
a different interpretation under negation as failure. For instance,
if ?X is bound and ?Y is unbound then
p(?X) :- naf q(?X,?Y)
is actually supposed to mean
forall ?X ( p(?X) :- naf exist ?Y q(?X,?Y) )
If we allow explicit universal quantification in the rule bodies then
implicit existential quantification is not enough and explicit existential
quantifier is needed. This is because forall
and exist do not
commute and so, for example, forall ?X exist ?Y and
exist ?Y forall ?X mean different things. If only implicit
existential quantification were available, it would not be possible to
differentiate between the above two forms.
Formally, the Nonmonotonic Lloyd-Topor layer permits the following kinds of rules. The rule heads are the same as in the monotonic LT extension. The rule bodies are defined as follows.
and g
or g
naf f
==> g
<== g
<==> g
exist ?X1,...,?Xn(f)
?X1, ..., ?Xn are variables that occur
positively (defined below) in f.
forall
?X1,...,?Xn(g1 ==> g2)
forall
?X1,...,?Xn(g2 <== g1)
?X1,
..., ?Xn occur positively in g1
Positive occurrence of a free variable in a formula is defined as follows:
and g
iff it occurs positively in either f or g.
or g
iff it occurs positively in both f and g.
==> g iff it occurs positively
in g. Similarly for f <== g,
except that now the variable must occur positively in f.
Since f <==> g is a conjunction of two
clauses, the definition of positive occurrence follows from the previous
cases: the variable must occur positively in f or g.
exist
?X1,...,?Xn(f) or
forall ?X1,...,?Xn(f) iff it
occurs positively in f.
The semantics of Lloyd-Topor extensions is defined via a transformation into the NAF layer as shown below. The theory behind this transformation is described in [Lloyd87].
Lloyd-Topor transformation: The transformation is designed to eliminate the extended forms that may occur in the bodies of the rules compared to the NAF layer. These extended forms involve the various types of implication and the explicit quantifiers. Note that the rules, below, must be applied top-down, that is, to the conjuncts that appear directly in the rule body. For instance, if the rule body looks like
:- ... and ((forall X exist Y (foo(Y,Y) ==> bar(X,Z)))
<== foobar(Z)) and ...
then one should first apply the rule for <==, then the
rules for forall should be applied to the result, and finally the
rules for exist.
Let the rule be of the form
:-
body1 and (f ==> g)
and body2.
Then the LT transformation replaces it with the following pair of rules:
:-
body1 and naf f
and body2.
:-
body1 and g
and body2.
The transformations for <== and <==> are similar.
Let the rule be
:-
body1 and
forall
?X1,...,?Xn(g1 ==> g2)
and body2.
?X1,...,?Xn are free variables
that occur positively in g1.
The LT transformation replaces this rule with the following pair of
rules, where
q(?X'1,...,?X'n) is a new
predicate of arity n
and ?X'1,...,?X'n are new variables:
:-
body1 and
naf
q(?X'1,...,?X'n)
and body2
q(?X1,...,?Xn) :-
g1 and naf g2.
The transformation for <== is similar.
Let the rule be
:-
body1 and
exist
?X1,...,?Xn(f)
and body2.
where ?X1,...,?Xn are free variables
that occur positively in f.
The LT transformation replaces this rule with the following:
:-
body1 and
f
and body2
That is, explicit existential quantification can be replaced in this case with implicit quantification.
The above transformations are inspired by (but are not derived from, due to a
significant difference between naf and neg!) the
classical tautologies (f ==> g) <==>
(neg f or g) and forall X (f) <==>
neg exist neg X (f), and by the fact mentioned in
section The NAF Layer that naf
p(X), when X does not occur anywhere else in the rule, is
interpreted as forall X (naf p(X)).
HiLog [Chen93] extends the first-order syntax with higher-order features. In particular, it allows variables to range over function symbols, predicate symbols, and even atomic formulas. These features are useful for supporting reification and in cases when an agent needs to explore the structure of an unknown piece of knowledge. HiLog further supports parameterized predicates, which are useful for generic definitions (illustrated below).
t(t1,...,tn), where
t, t1, ..., tn are
HiLog terms.
This definition may seem quite similar to the definition of complex
first-order terms, but, in fact, it defines a vastly larger set of
expressions. In first-order terms, t must be a constant, while in
HiLog it can be any HiLog term. In particular, it can be a variable or even
another first-order term. For instance, the following are legal HiLog terms:
c, f(a,?X), ?X
?X(a,?Y), ?X(a,?Y(?X))
f(?X,a)(b,?X(c)), ?Z(?X,a)(b,?X(?Y)(d)), ?Z(f)(g,a)(p,?X)
We will see soon how such terms can be useful in knowledge representation.
Thus, expressions like ?X(a,?Y(?X)) are atomic
formulas and thus can have truth values (when the variables are
instantiated or quantified). What is less obvious is that
?X is also an atomic formula. What all this means is that
atomic formulas are automatically reified and can be passed around by binding
them to variables and evaluated. For instance, the following HiLog query
?- q(?X) and ?X.
p(a).
q(p(a)).
succeeds with the above database and ?X gets bound
to p(a).
Another interesting example of a HiLog rule is
call(?X) :- ?X.
This can be viewed as a logical definition of the
meta-predicate call/1 in Prolog. Such a definition does not make
sense in first-order logic (and is, in fact, illegal), but it is legal in HiLog
and provides the expected semantics for call/1.
We will now illustrate one use of the parameterized predicates of the
form p(...)(...). The example shows a pair of rules that defines
a generic transitive closure of a binary predicate.
Depending on the actual predicate passed in as a parameter, we can get
different transitive closures.
closure(?P)(?X,?Y) :- ?P(?X,?Y).
closure(?P)(?X,?Y) :- ?P(?X,?Z) and closure(?P)(?Z,?Y).
For instance, for the parent
predicate, closure(parent) is defined by the above rules to be
the ancestor relation; for the edge relation that represents
edges in a graph, closure(edge) will become the transitive
closure of the graph.
This layer introduces the full equality
predicate, :=:.
The equality predicate obeys the usual
congruence axioms for equality. In particular, it is transitive,
symmetric, reflexive, and the logical entailment relation is invariant
with respect to the substitution of equals by equals. For instance, if
we are told that bob :=: father(tom) (bob is
the same individual as the one denoted by the
term father(tom)) then if p(bob) is known to be
true then we should be able to derive
p(father(tom)). If we are also told that bob
:=: uncle(mary) is true then we can derive father(tom):=:
uncle(mary).
Equality in a Semantic Web language is important to be able to state that two different identifiers represent the same resource. For that reason, equality was part of OWL [OWL Reference]. Although equality drastically increases the computational complexity, some forms of equality, such as ground equality, can be handled efficiently in a rule-based language.
The equality predicate :=: is different from the unification
operator = in several respects. First, for variable free
terms, term1 = term2
if and only if the two terms are identical. In contrast, as we have just
seen, two distinct terms can be equal with respect
to :=:. Since :=: is reflective, it follows
that the interpretation of :=: always contains the
interpretation of =. Second, the unification
operator = cannot appear in a rule head, while the equality
predicate :=: can. When :=: occurs in the rule
head (or as a fact), it is an assertion (maybe conditional) that two
terms are equal. For instance, given the above definitions,
p(1,2).
p(2,3).
f(a,?X):=:g(?Y,b) :- p(?X,?Y).
entails the following equalities between distinct
terms: f(a,1):=:g(2,b) and
f(a,2):=:g(3,b).
When term1 :=: term2 occurs
in the body of a rule and term1
and term2 have variables, this predicate is interpreted as
a test that there is a substitution that makes the two terms equal with
respect to :=: (note: equal, not identical!). For instance,
in the query
q(1).
q(2).
q(3).
?- f(a,?X):=:g(?Y,b) and q(?Y).
one answer substitution is ?X/1,?Y/2 and the other is
?X/2,?Y/3.
The Frames layer introduces object-oriented syntax modeled after F-logic [Kifer95] and its subsequent enhancements [Yang02, Yang03]. The main syntactic additions of this layer include
The object-oriented extensions introduced by the Frames layer are orthogonal to the other layers described so far and can be combined with them within the SWSL-Rules language.
As in most object-oriented languages, the three main concepts in the Frames layer of SWSL-Rules are objects, classes, and methods. (We are borrowing from the object-oriented terminology here rather than AI terminology, so we are refer to methods rather than slots.) Any class is also an object, and the same expression can denote an object or a class represented by this object in different contexts.
A method is a function that takes arguments and executes in the context of a particular object. When invoked, a method returns a result and can possibly alter the state of the knowledge base. A method that does not take arguments and does not change the knowledge base is called an attribute. An object is represented by its object Id, the values of its attributes, and by the definitions of its methods. Method and attribute names are represented as objects, so one can reason about them in the same language.
An object Id is syntactically represented by a ground term. Terms that do have variables are viewed as templates for collections of object Ids—one Id per ground instantiation of all the variables in the term. By term we mean any expression that can bind a variable. What constitutes a legal term depends on the layer. In the basic case, by term we mean just a first-order term. If the Frames layer is combined with HiLog, then terms are meant to be HiLog terms. Later, when we introduce reification, reification terms will also be considered.
Molecules. Molecules play the role of atomic formulas. We first describe atomic molecules and then introduce complex molecules. Although both atomic and complex molecules play the role of atomic formulas, complex molecules are not indivisible. This is why they are called molecules and not atoms. Molecules come in several different forms:
t, m, v are terms then t[m
-> v] is a value molecule.
Here t denotes an object, m denotes
a method invocation in the scope of the
object t, and v denotes a value that
belongs to a set returned by
this invocation. We call m ``a
method invocation'' because if
m = s(t1,...,tn), i.e., has
arguments, then
t[s(t1,...,tn) -> v] is
interpreted as an invocation of method s on
arguments t1,...,tn in the context of
the object
t, which returns a set of values that
contains v.
The syntax t[m -> {v1,...,vk}] is
also supported; it means that if m is invoked in the
context of the object t then it returns a set that
contains v1,...,vk. Thus,
semantically, such a term is equivalent to a conjunction of t[m
-> v1], ..., t[m ->
vk], so the expressions t[m ->
{v1,...,vk}] is just a syntactic sugar.
t[m] where t and m are
terms.
Boolean molecules are useful to specify things like
mary[female]. The same could be alternatively written as
mary[female -> true], but this is less natural.
t and s
are terms then t:s is a membership molecule.
If t and s are variable free, then such a
molecule states that the object t is a member of
class s. If these terms contain variables, then such a
molecule can be viewed as many class membership
statements, one per ground instantiation of the variables.
t and s are terms
then t::s is a subclass molecule.
If t and s are variable free, then such a
molecule states that the object t is a subclass
of s. As in the case of class membership molecules,
subclass molecules that have variables can be viewed as statements about
many subclass relationships.
t, m, v are terms then t[m
=> v] is a signature molecule.
If t, m, and v are variable-free
terms then the informal meaning of the above signature molecule is
that t represents a class, which has a method
invocation m which returns a set of objects of
type v (i.e., each object in the set belongs to
class v).
If these terms are non-ground then the signature represents a collection
of statements—one statement per ground instantiation of the terms.
When m itself has arguments, for instance m =
s(t1,...,tn), then the arguments are
interpreted
as types. Thus, t[s(t1,...,tn) =>
v] states that when the n-ary method s
is invoked on object of class t with
arguments that belong to
classes t1,
..., tn, the
method returns a set of objects of class v.
t[m=>]. Its purpose is to provide type
information for Boolean valued molecules. Namely, if
m=s(t1,...,tn), then when the method
s is
invoked on an object of class t, the method arguments must
belong to classes t1,
..., tn.
Cardinality constraints: Signature molecules can have associated cardinality constraints. Such molecules have the form
t[s(t1,...,tn) {min : max}
=> v]
where min and max are non-negative integers such that
min ≤ max. Max can also be *, which
means positive infinity.
Such a signature states not only that the invocation
of the method s with arguments of type
t1,...,tn on an object of
class t returns objects of class v, but also that
the number of such objects in the result is no less than min and
no more than max.
The semantics of constraints in SWSL-Rules is similar to constraints in databases and is unlike the cardinality restrictions in OWL [OWL Reference]. For instance, if a cardinality constraint says that an attribute should have at least two values and the rule base derives only one then the constraint is violated. In contrast, OWL would infer that there is another, yet unknown, value. Likewise, if a cardinality constraint says that the number of elements is at most three while the rule base derives four unequal elements then the constraint is, again, violated. This should be compared to the OWL semantics, which will infer that some pair of derived values in fact consists of equal elements.
Signatures and type checking: Signatures are assertions about the expected types of the method arguments and method results. They typically do not have direct effect on the inference (unless signatures appear in rule bodies). The signature information is optional.
The semantics of signatures is defined as follows. First, the intended model of the knowledge base is computed (which in SWSL-Rules is taken to be the well-founded model). Then, if typing needs to be checked, we must verify that this intended model is well-typed. A well-typed model is one where the value molecules conform to their signatures. For the precise definition of well-typed models see [Kifer95]. (There can be several different notions of well-typed models. For instance, one for semi-structured data and another for completely structured data.)
A type-checker can be written in SWSL-Rules using just a few rules. Such a type checker is a query, which returns "No", if the model is well-typed and a counterexample otherwise. In particular, type-checking has the same complexity as querying. An example of such type checker can be found in the FLORA-2 manual [Yang04].
It is important to be aware of the fact that the semantics of the
cardinality constraints in signature molecules
is inspired by database theory and practice
and it is different from the semantics of such constraints in OWL
[OWL Reference]. In SWSL-Rules, cardinality constraints are restrictions on the
intended models of the knowledge base, but they are not part of the axioms
of the
knowledge base. Therefore, the intended models of the knowledge base
are determined without taking the cardinality constraints into the account.
Intended models that do not satisfy these restrictions are
discarded. In contrast, in OWL cardinality constraints are represented as
logical statements in the knowledge base and all models are computed by
taking the constraints into the account. Therefore, in OWL it is not
possible to talk about knowledge base updates that violate constraints.
For instance, the following signature married[spouse {1:1} =>
married] states that every married person has exactly one spouse.
If john:married is true but there is no information about
John's spouse then OWL will assume that john has some unknown
spouse, while SWSL-Rules will reject the knowledge base as inconsistent.
If, instead, we know that john[spouse -> mary] and
john[spouse -> sally] then OWL will conclude that
mary and sally are the same object, while
SWSL-Rules will again rule the knowledge base to be inconsistent (because,
in the absence of the information to the contrary — for example, if
no :=:-statements have been given — mary
and sally will be deemed to be distinct objects).
Inheritance in SWSL-Rules: Inheritance is an optional feature, which is expressed by means of the syntactic features described below. In SWSL-Rules, methods and attributes can be inheritable and non-inheritable. Non-inheritable methods/attributes correspond to class methods in Java, while inheritable methods and attributes correspond to instance methods.
The value- and signature-molecules considered so far
involve non-inheritable attributes and methods. Inheritable methods
are defined using the *-> and *=> arrow
types, i.e.,
t[m *-> v] and t[m *=> v]. For Boolean
methods we use
t[*m] and t[m*=>].
Signatures obey the laws of monotonic inheritance, which are as follows:
t:s and s[m *=> v] entails t[m *=> v]
t::s and s[m *=> v] entails t[m => v]
These laws state that type declarations for inheritable methods are inherited to subclasses in an inheritable form, i.e., they can be further inherited. However, to the members of a class such declarations are inherited in a non-inheritable form. Thus, inheritance of signatures is propagated through subclasses, but stops once it hits class members.
Inheritance of value molecules is more involved. This type of inheritance is nonmonotonic and it can be overridden if the same method or attribute is defined for a more specific class. More precisely,
t:s and s[m *-> v] entails t[m *-> v]
unless overridden or in conflict
t::s and s[m *-> v] entails t[m -> v]
unless overridden or in conflict
Similarly to signatures, value molecules are inherited to subclasses in the
inheritable form and to members of the classes in the non-inheritable form.
However, the key difference is the phrase "unless overridden or in conflict."
Intuitively, this means that if, for example, there is a class w
in-between t and s such that the inheritable method
m is defined there then the inheritance from s is
blocked and m should be inherited from w instead.
Another situation when inheritance might be blocked arises due to multiple
inheritance conflicts. For instance, if t is a subclass of both
s and u, and if both s
and u define the method m, then inheritance
of m does not take place at all (either from s or
from u; this policy can be modified by specifying appropriate
rules, however). The precise model-theoretic semantics of inheritance with
overriding is based on an extended form of the Well-Founded Semantics.
Details can be found in
[Yang02].
Note that signature inheritance is not subject to overriding, so every inheritable molecule is inherited to subclasses and class instances. If multiple molecules are inherited to a class member or a subclass, then all of them are considered to be true.
Inheritance of Boolean methods is similar to the inheritance of methods and attributes that return non-Boolean values. Namely,
t:s and s[m*=>] entails t[m*=>]
t::s and s[m*=>] entails t[m =>]
t:s and s[*m] entails t[*m]
unless overridden
t::s and s[*m] entails t[m]
unless overridden
Complex molecules: SWSL-Rules molecules can be combined into complex molecules in two ways:
Grouping applies to molecules that describe the same object. For instance,
t[m1 -> v1] and t[m2 => v2] and t[m3 {6:9} => v3] and t[m4 -> v4]
is, by definition, equivalent to
t[m1 -> v1 and m2 => v2 and m3 {6:9} => v3 and m4 -> v4]
Molecules connected by the or connective can also be combined
using the usual precedence rules:
t[m1 -> v1] and t[m2 => v2] or t[m3 {6:9} => v3] and t[m4 -> v4]
becomes
t[m1 -> v1 and m2 => v2 or m3 {6:9} => v3 and m4 -> v4]
The and connective inside a complex molecule can also be
replaced with a comma, for brevity. For example,
t[m1 -> v1, m2 => v2]
Nesting applies to molecules in the following ``chaining'' situation, which is a common idiom in object-oriented databases:
t[m -> v] and v[q -> r]
is by definition equivalent to
t[m -> v[q -> r]]
Nesting can also be used to combine membership and subclass molecules with value and signature molecules in the following situations:
t:s and t[m -> v]
t::s and t[m -> v]
are equivalent to
t[m -> v]:s
t[m -> v]::s
respectively.
Molecules can also be nested inside predicates and terms with
a semantics similar to nesting inside other molecules. For instance,
p[a->c] is considered to be equivalent to
p(a) and a[b->c]. Deep nesting and, in fact, nesting in any
part of another molecule or predicate is also allowed. Thus, the
formulas
p(f(q,a[b -> c]),foo)
a[b -> foo(e[f -> g])]
a[foo(b[c -> d]) -> e]
a[foo[b -> c] -> e]
a[b -> c](q,r)
are considered to be equivalent to
p(f(q,a),foo) and a[b -> c]
a[b -> foo(e)] and e[f -> g]
a[foo(b) -> e] and b[c -> d]
a[foo -> e] and foo[b -> c]
a[b -> c] and a(q,r)
respectively. Note that molecule nesting leads to a completely
compositional syntax, which in our case
means that molecules are allowed in any place where terms are allowed.
(Not all of these nestings might look particularly natural, e.g., a[b
-> c](q,r) or p(a[b -> c](?X)), but there is no
good reason to reject these nestings and thus complicate the syntax either.)
Path expressions: Path expressions are useful shorthands that are widely used in object-oriented and Web languages. In a logic-based language, a path expression sometimes allows writing formulas more concisely by eliminating multiple nested molecules and explicit variables. SWSL-Rules defines path expressions only as replacements for value molecules, since this is where this shorthand is most useful in practice.
A path expression has the form
t.t1.t2. ... .tn
or
t!t1!t2! ... !tn
The former corresponds to non-inheritable molecules and the latter to inheritable ones. In fact, "." and "!" can be mixed within the same path expression.
A path expression can occur anywhere where a term is allowed to occur. For
instance, a[b -> c.d], a.b.c[e ->
d], p(a.b), and X=a.b are all legal
formulas. The semantics of path expressions in the body of a rule and in its
head are similar, but slightly different. This difference is
explained next.
In the body of a rule, an occurrence of the first path expression above is treated as follows. The conjunction
t[t1 -> ?Var1] and
?Var1[t2 -> ?Var2] and ... and
?Varn-1[tn -> ?Varn]
is added to the body and the occurrence of the path expression is replaced with
the variable ?Varn. In this conjunction, the variables
?Var1, ..., ?Varn
are new and are used to represent intermediate values.
The second path expression is treated similarly, except that the conjunction
t[t1 *-> ?Var1] and
?Var1[t2 *-> ?Var2] and ... and
?Varn-1[tn *-> ?Varn]
is used. For instance, mary.father.mother = sally in a rule body
is replaced with
mary[father -> ?F] and ?F[mother -> ?M] and ?M = sally
In the head of a rule, the semantics of path expressions is reduced
to the case of a body occurrence as follows.. If a path
expression, ρ,
occurs in the head of a rule, it is replaced with a new
variable, ?V, and the predicate ?V=ρ is
conjoined to the body of the rule. For instance,
p(a.b) :- body.
is understood as
p(?V) :- body and ?V=a.b.
Note that since molecules can appear wherever terms can, path expressions of
the form a.b[c -> d].e.f[g -> h].k are permitted.
They are conceptually similar to XPath expressions with
predicates that control the selection of intermediate nodes in XML documents.
Formally, such a path expression will be replaced with the
variable ?V and will result in the addition of the following
conjunction:
a[b -> ?X[c -> d]] and ?X[e -> ?Y] and
?Y[f -> ?Z[g -> h]] and ?Z[k -> ?V]
It is instructive to compare SWSL-Rules path expressions with
XPath. SWSL-Rules path expressions were originally proposed for F-logic
[Kifer95] several years before XPath. The
purpose was to extend the familiar notation in object-oriented programming
languages and to adapt it to a logic-based language. It is easy to see that
the ``*'' idiom of XPath can be captured with the use of a variable. For
instance, b/*/c applied to object e is expressed
as e.b.?X.c. The ``..'' idiom of XPath is also easy to
express. For instance, a/../b/c applied to object d
is expressed as ?_[?_ -> d.a].b.c. On the other hand, there
is no counterpart for the // idiom of XPath. The reason is that
this idiom is not well-defined when there are cycles in the data (for
instance, a[b -> a]). However, recursive descent into the
object graph can be defined via recursive rules.
The reification layer allows SWSL-Rules to treat certain kinds of formulas as terms and therefore to manipulate them, pass them as parameters, and perform various kinds of reasoning with them. In fact, the HiLog layer already allows certain formulas to be reified. Indeed, since any HiLog term is also a HiLog atomic formula, such atomic formulas are already reifiable. However, the reification layer goes several steps further by supporting reification of arbitrary rule or formula that can occur in the rule head or rule body. (Provided that it does not contain explicit quantifiers -- see below.)
Formally, if F is a formula that has the syntactic form of a rule head, a rule body, or of a rule then F is also considered to be a term. This means that such a formula can be used wherever a term can occur.
Note that a reified formula represents an objectification of the corresponding formulas. This is useful for specifying ontologies where objects represent theories that can be true in some worlds, but are not true in the present world (and thus those theories cannot be asserted in the present world). Examples include the effects of actions: effects of an action might be true in the world that will result after the execution of an action, but they are not necessarily true now.
In general, reification of formulas can lead to logical paradoxes [Perlis85]. The form of reification used in SWSL-Rules does not cause paradoxes, but other unpleasantries can occur. For instance, the presences of a truth axiom (true(?X) <--> ?X) can render innocently looking rule-bases inconsistent. However, as shown in [Yang03], the form of reification in SWSL-Rules does not cause paradoxes as long as
?X :- body (which are legal in HiLog) are
disallowed.
We therefore adopt the above restrictions for all layers of SWSL-Rules (but not for SWSL-FOL).
As presented above, reification introduces syntactic ambiguity, which arises due to the nesting conventions for molecules. For instance, consider the following molecule:
a[b -> t]
Suppose that t is a reification of another
molecule, c[d -> e]. Since we have earlier said that
any formula suitable to appear in the rule body can also be viewed as a
term, we can expand the above formula into
a[b -> c[d -> e]]
But this is ambiguous, since earlier we defined the above as a commonly used object-oriented idiom, a syntactic sugar for
a[b -> c] and c[d -> e]
Similarly, if we want to write something like t[b -> c]
where t is a reification of f[g -> h] then we
cannot write f[g -> h][b -> c]
because this nested molecule is a syntactic sugar for f[g -> h]
and f[b -> c].
To resolve this ambiguity, we introduce the reification
operator, ${...}, whose only role is to tell the parser that
a particular occurrence of a nested molecule is to be treated as
a term that represents a reified formula rather than
as syntactic sugar for the object-oriented idiom.
Note that the explicit reification operator is not required for HiLog
predicates because there is no ambiguity. For instance, we do not need to
write ${p(?X)} below (although it is permitted and
is considered the same as p(?X)):
a[b -> p(?X)]
This is because a[b -> p(?X)] does not mean
a[b -> p(?X)] and p(?X), since the sugar is used
only for nested molecules.
In contrast, explicit reification is needed below, if we want to reify
p(?X[foo -> bar]):
a[b -> p(?X[foo -> bar])]
Otherwise p(?X[foo -> bar]) would be treated as syntactic
sugar for sugar for
a[b -> p(?X)] and ?X[foo -> bar]
Therefore, to reify p(?X[foo -> bar]) in the above
molecule one must write this instead:
a[b -> ${p(?X[foo -> bar])}]
Example. Reification in SWSL-Rules is very powerful and yet it doesn't add to the complexity of the language. The following fragment of a knowledge base models an agent who believes in the modus ponens rule:
john[believes -> ${p(a)}].
john[believes -> ${p(?X) ==> q(?X)}].
// modus ponens
john[believes -> ?A] :-
john[believes -> ${?B ==> ?A}] and john[believes -> ?B].
Since the agent believes in p(a) and in the modus ponens
rule, it can infer q(a). Note that in the above we did not
need explicit reification of p(a), since no ambiguity can
arise. However, we used the explicit reification anyway, for clarity.
Syntactic rules. Currently SWSL-Rules does not permit explicit quantifiers under the scope of the reification operator, because the semantics for reification given in [Yang03, Kifer04] does not cover this case. So not every formula can be reified. More specifically, the formulas that are allowed under the scope of the reification operator are:
The implication of these restrictions is that every term that represents a reification of a SWSL-Rules formula has only free variables, which can be bound outside of the term. Each such term can therefore be viewed as a (possibly infinite) set of reifications of the ground instances of that formula.
It is often necessary to specify existential information in the head of a rule
or in a fact. Due to the limitations of the logic programming paradigm, which
trades the expressive power for executional efficiency, such information
cannot be specified directly. However, existential variables in the rule heads
can be approximated through the technique known as Skolemization
[Chang73].
The idea of Skolemization is that in a formula of the form
∀ Y1...Yn∃ X ... φ
the existential variable X can be removed and replaced
everywhere in φ with the function
term f(Y1...Yn), where f is a
new function symbol that does not occur anywhere else in the
specification. The rationale for such a substitution is that,
for any query, the original rule
base is unsatisfiable if and only if the transformed rule base is
unsatisfiable
[Chang73].
This implies that the query to the original rule base can be answered if and
only if it can be answered when posed against the Skolemized rule base.
However, from the point of view of logical entailment, the Skolemized
rule base is stronger than the original one, and this is why we say that
Skolemization only approximates existential quantification, but is
not equivalent to it.
Skolemization is defined for formulas in prenex normal form, i.e., formulas where all the quantifiers are collected in a prefix to the formula and apply to the entire formula. A formula that is not in the prenex normal form can be converted to one in the prenex normal form by a series of equivalence transformations [Chang73].
SWSL-Rules supports Skolemization by providing special constants
_# and _#1, _#2, _#3,
and so on. As with other constants in SWSL, these symbols can be used
both in argument positions and in the position of a
function. For instance, _#(a,_#,_#2(c,_#2)) is a legal function term.
Each occurrence of the symbol _# denotes a new
constant. Generation of such a constant is the responsibility of the
SWSL-Rules compiler. For instance, in _#(a,_#,_#2(c,_#2)),
the two occurrences of _# denote two different constants
that do not appear anywhere else. In the first case, the constant is in
the position of a function symbol. The numbered Skolem constants, such
as _#2 in our example, also denote a new constant that does
not occur anywhere else in the rule base. However, the different
occurrences of the same numbered symbol in the same rule denote
the same new constant. Thus, in the above example the two
occurrences of _#2 denote the same new symbol. Here is a
more complete example:
holds(a,_#1) and between(1,_#1,5).
between(minusInf, _#(?Y), ?Y) :- timepoint(?Y) ?Y !=
minusInf.
In the first line, the two occurrences of _#1 denote the
same new Skolem constant, since they occur in the scope of the same
rule. In the second line, the occurrence of _# denotes a new
Skolem function symbol. Since we used _# here, this symbol
is distinct from any other constant. Note, however, that even if we
used _#1 in the second rule, that symbol would have denoted
a distinct new function symbol, since it occurs in a separate rule and
there is no other occurrence of _#1 in that rule.
The Skolem constants in SWSL-Rules are in some ways analogous to the blank nodes in RDF. However, they have the semantics suitable for a rule-based language and it has been argued in [Yang03] that the Skolem semantics is superior to RDF, which relies on existential variables in the rule heads [Hayes04].
SWSL-Rules supports the primitive XML Schema data types. However, since SWSL-Rules is quite different from XML, it adapts the lexical representation for XML data types to the form that is more suitable for a logic-based language. The translation from the XML lexical representation of primitive data types to SWSL-Rules is straightforward.
The general rule is that each primitive value is represented by a function
term whose functor symbol is the name of the primitive data type prefixed with
an underscore (_). The arguments of the term represent the various
components of the primitive data type. For
instance, _string("abc"), _date(2005,7,18),
_decimal(123.56), _integer(321),
_float(23e5), and so on.
The string, decimal, integer, and float data types have a shorthand notation
(some of which had been seen before). Thus, _string("abc") is
abbreviated to "abc", _decimal(123.56)
to 123.56, _integer(321) to 321,
and _float(23e5) to 23e5.
Other primitive data types are represented using a similar notation. For
instance, the duration of 1 year, 2 months, 3 days, 10 hours, and 30 minutes
is represented as _duration(1,2,3,10,30,0) where the first
argument of _duration represents years and the last seconds. The
same negative duration is represented
as -_duration(1,2,3,10,30,0).
For another example, the
values of the dateTime type are represented as
_dateTime(2005,10,29,15,55,40).
It is often necessary to exchange values of primitive data types
between applications. Since the internal representations of the data types
vary from language to language, serialization into a commonly
agreed representation has been used for this purpose. SWSL-Rules supports
serialization of primitive data types via the built-in
predicate _serialize. It takes three arguments: a SWSL-Rules
value of a SWSL-Rules data type, a URI that denotes the target of
serialization, and a result, which is a string that contains the serialized
value. Currently, the only target
is http://www.w3.org/2001/XMLSchema, which refers to XML Schema
1.0. Other targets will be added as necessary (for example, for XML
Schema 1.1 when it is released). Example:
_serialize(_date(2005,1,1),_"http://www.w3.org/2001/XMLSchema",?Result)
binds ?Result to "2005-01-01".
The predicate _serialize is intended to work both ways: for
serialization and deserialization. Deserialization occurs when the last
argument is bound to a string representation of a data type and the first
argument is unbound. For instance,
_serialize(?Result,_"http://www.w3.org/2001/XMLSchema","2005-01-01")
binds ?Result to _date(2005,1,1).
A single point of reference for the model-theoretic semantics of SWSL-Rules will be given in a separate document. Here we will only give an overview and point to the papers where the semantics of the different layers were defined separately.
First, we note that the semantics of the Lloyd-Topor leyers -- both monotonic and nonmonotonic -- is transformational and was given in Sections 2.4 and 2.6. Similarly, the Courteous layer is defined transformationally and is described in [Grosof2004a].
The model theory of NAF is given by the well-founded semantics as described in [VanGelder91]. The model theory behind HiLog is described in [Chen93] and F-logic is described in [Kifer95]. The semantics of inheritance that is used in SWSL-Rules is defined in [Yang02]. The model theory of reification is given in [Yang03] and was further extended to reification of rules in [Kifer04].
The semantics of the Equality layer is based on the standard semantics (for
instance, [Chang73]) but is modified
by the unique name assumption, which states that
syntactically distinct terms are unequal. This modification is described in
[Kifer95], and we summarize it here.
First, without equality, SWSL-Rules makes the unique name assumption. With
equality, the unique name assumption is modified to say that terms that
cannot be proved equal with respect to :=: are assumed to be
unequal. In other words, SWSL-Rules makes a closed world assumption about
explicit equality.
Other than that, the semantics of :=: is standard. The
interpretation of this predicate is assumed to be an equivalence relation
with congruence properties. A layman's term for this
is "substitution of equals by equals." This means that if, for
example,
t:=:s is derived for some terms t
and s then, for any formula φ, it is true if and only if
ψ is true, where ψ is obtained from φ by replacing some
occurrences of t with s.
Overall, the semantics of SWSL-Rules has nonmonotonic flavor even without NAF and its extension layers. This is manifested by the use of the unique name assumption (modified appropriately in the presence of equality) and the treatment of constraints. To explain the semantics of constraints, we first need to explain the idea of canonic models.
In classical logic, all models of a set of formulas are created equal and are given equal consideration. Nonmonotonic logics, on the other hand, carefully define a subset of models, which are declared to be canonical and logical entailment is considered only with respect to this subset of models. Normally, the canonical models are so-called minimal models, but not all minimal models are canonical.
Any rule set that does not use the features of the NAF layer and its extensions is known to have a unique minimal model, which is also its canonical model. This is an extension of the well-known fact for Horn clauses in classical logic programming [Lloyd87]. With NAF, a rule set may have multiple incomparable minimal models, and it is well-known that not all of these models appropriately capture the intended meaning of rules. However, it turns out that one such model can be distinguished, and it is called the well-founded model [VanGelder91]. A formula is considered to be true according to the SWSL-Rules semantics if and only if it is true in that one single model, and the formula is false if and only if it is false in that model.
Now, in the presence of constraints, the semantics of SWSL-Rules is defined as follows. Given a rulebase, first its canonical model is determined. In this process, all constraints are ignored. Next, the constraints are checked in the canonical model. If all of them are true, the rulebase is said to be consistent. If at least one constraint is false in the canonical model, the constraint is said to be violated and the rulebase is said to be inconsistent.
The SWSL language includes all the connectives used in first-order logic and,
therefore, syntactically first-order logic is a subset of SWSL.
When the semantics of first-order connectives differs from their
nonmonotonic interpretation, new nonmonotonic connectives are
introduced. For instance, first-order negation, neg, has a
nonmonotonic counterpart naf and first-order implications
<==
and ==> have a nonmonotonic counterpart :-.
It follows from the above that SWSL-Rules and SWSL-FOL share
significant portions of their syntax. In particular, every connective
used in SWSL-FOL can also be used in SWSL-Rules. However, not every
first-order formula in SWSL-FOL is a rule and the rules in SWSL-Rules are
not first-order formulas (because of ":-"). Therefore,
neither SWSL-FOL is a subset of SWSL-Rules nor the other way
around. Furthermore, even though the classical connectives
neg and ==>/<== can
occur in SWSL-Rules, they are embedded into an overall nonmonotonic
language and their semantics cannot be said to be exactly first-order.
Formally, SWSL-FOL consists of the following formulas:
and ψ, φ or ψ,
neg φ, φ ==> ψ,
φ <== ψ, and φ <==>
ψ.
X is a variable, then
the following are also SWSL-FOL formulas: exist ?X
(φ) and forall ?X (φ). SWSL-FOL
allows to combine quantifiers of the same sort, so exist
?X,?Y (φ) is the same as
exist ?X exist ?Y (φ).
As in the case of SWSL-Rules, we will ise the period (".") to designate the end of a SWSL-FOL formula.
SWSL defines three extensions of SWSL-FOL. The first extension adds
the equality operator, :=:, the second incorporates the
object-oriented syntax from the Frames layer of SWSL-Rules, the third does
the same for the HiLog layer.
Formally, SWSL-FOL+Equality has the same syntax as SWSL-FOL, but, in addition, the following atomic formulas are allowed:
SWSL-FOL+Frames has the same syntax as SWSL-FOL except that, in addition, the following is allowed:
SWSL-FOL+HiLog extends SWSL-FOL by allowing HiLog terms and HiLog atomic formulas instead of first-order terms and first-order atomic formulas.
Each of these extensions is not only a syntactic extension of SWSL-FOL but
also a semantic extension. This means that if φ and ψ are formulas
in SWSL-FOL
then φ |= ψ in SWSL-FOL if and only if the
same holds in SWSL-FOL+Equality, SWSL-FOL+Frames, and SWSL-FOL+HiLog.
We will say that SWSL-FOL+Equality, SWSL-FOL+Frames, and SWSL-FOL+HiLog are
conservative semantic extensions of SWSL-FOL.
SWSL-FOL+HiLog and SWSL-FOL+Frames can be combined both syntactically and
semantically. The resulting language is a conservative semantic extension of
both SWSL-FOL+HiLog and SWSL-FOL+Frames. Similarly, SWSL-FOL+Equality and
SWSL-FOL+Frames can be combined and the resulting language is a conservative
extension of both. Interestingly, combining SWSL-FOL+Equality with
SWSL-FOL+HiLog leads to a conservative extension of
SWSL-FOL+HiLog, but not of SWSL-FOL+Equality!
More precisely, if φ and ψ are formulas in SWSL-FOL+Equality
and φ |= ψ then the same holds in
SWSL-FOL+HiLog. However, there are formulas such that φ |=
ψ holds in SWSL-FOL+HiLog but not in SWSL-FOL+Equality
[Chen93].
The semantics of the first-order sublanguage of SWSL is based on the standard first-order model theory and is monotonic. The only new elements here are the higher-order extension that is based on HiLog [Chen93] and the frame-based extension based on F-logic [Kifer95]. The respective references provide a complete model theory for these extensions, which extends the standard model theory for first-order logic.
To enhance the power of the SWSL-Rules language, a number of extensions are being planned, as described below.
If-then-else. The if test
then test1 is sometimes more convenient and familiar
than the ==> operator. More important, however, is the
fact that the more complete idiom, if test
then test1 else test2, is known to be
very useful and common in rule-based languages. Although
the else-part can be expressed with negation as failure,
this is not natural and most well-developed languages support
the if-then-else idiom directly. This idiom may be added to
SWSL-Rules later.
Aggregate operators. Aggregate operators, such as sum, average, etc., are important database operations. XML languages such as XPath, XSLT, and XQuery all have support for aggregation. Of these, only XQuery permits aggregation over general set comprehension. A future extension of SWSL-Rules will allow aggregation in the style of FLORA-2, which supports explicit set comprehension and nested aggregation. The general syntax of such aggregation is:
?Result = aggregate{?Var [GroupingVarList] | Query }
where aggregate can
be max, min, avg, count,
sum, collectset, collectbag. The
last two aggregates return lists of the instantiations
of ?Var that satisfy Query without the duplicates
(collectset) and with possible duplicates
(collectbag).
The grouping variables provide the functionality similar to GROUP
BY of SQL. They have the effect that the aggregation produces one list
of results per every instantiation of the variables
in GroupingVarList for which Query has a solution. The
variable ?Result gets successively bound to each such list (one
list at a time).
Constraints. Constraints play a very important role in database and knowledge base applications. As a future extension, SWSL-Rules will have database-style constraints. Database constraints are different in nature from restrictions used in Description Logic. Whereas restrictions in Description Logic are part of the same logical theory as the rest of the statements and are used to derive new statements, constraints in databases are not used to derive new information. Instead, they serve as tests of correctness for the canonical models of the knowledge base. In this framework, canonical models (e.g., the well-founded model [VanGelder91]) are first computed without taking constraints into account. These models are then checked against the constraints. The models that do not satisfy the constraints are discarded. In the case of the well-founded semantics, which always yields a single model, testing satisfaction of the constraints validates whether the knowledge base is in a consistent state.
Procedural attachments, state changes à la Transaction Logic, situated logic programs. A procedural attachment is a predicate or a method that is implemented by an external procedure (e.g., in Java or Python). Such a procedure can have a side effect on the real world (e.g., sending an email or activating a device) or it can receive information from the outside world. First formalizations of these ideas in the context of database and rule based languages appeared in [Maier81, Chimenti89]. These ideas were recently explored in [Grosof2004a] in the context of e-commerce. Transaction Logic [Bonner98] provides a seamless integration of these concept into the logic.
An attached procedure can be specified by a link statement, which associates a predicate or a method with an external program. The exact details of the syntax have not been finalized, but the following is a possibility:
attachment relation/Arity name-of-java-procedure(integer,string,...)
This syntax can be generalized to include object-oriented methods.
Another necessary extension involves update primitives - primitives for changing the underlying state of the knowledge. These primitives can add or delete facts, and even add or delete rules. A declarative account of such update operations in the context of a rule-based language is given by Transaction Logic [Bonner98]. This logic also can also be used to represent triggers (also known as ECA rules) [Bonner93].
Predicates with named arguments.
For predicates with ordered arguments,
named attributes are essentially supported by the current syntax.
For instance, if -> is viewed as an infix binary function symbol, then
p(foo -> 1, bar -> 2) is a valid term in SWSL-Rules.
Predicates with unordered arguments can make unification exponential
and are unlikely to be supported in the future.
The "rest"-variables. The ``rest'' notation à la SCL can be useful in metaprogramming. A rest-variable binds to a list of variables or terms and it always occurs as the last variable of a term. During unification with another term, such a variable binds to a list of arguments of that term beginning with argument corresponding to the variable till the rest of the term (whence the name of such variables). For instance, in the following term, ?R is a rest-variable:
p(?X,?Y | ?R)
If this term is unified
with p(?Z,f,?Z,q), then ?X binds
to ?Z, ?Y to f, and ?R
to the list [?Z,q].